Реклама

Колеса для большегрузных и платформенных тележек колеса для тележек.

Наш канал:

Таненбаум Э.- Архитектура компьютера. стр.124

В качестве примера использования булевой алгебры рассмотрим схему и таблицу истинности для функции АВ + АС (рис. 3.5, а). Хотя мы это еще не обсуждали, многие правила обычной алгебры имеют силу и в булевой алгебре. Например, выражение АВ + АС по дистрибутивному закону может быть преобразовано в А(В + С). На рис. 3.5, б показана схема и таблица истинности для функции А(В + С). Две функции являются эквивалентными тогда и только тогда, когда обе функции принимают одно и то же значение для всех возможных переменных. Из таблиц истинности на рис. 3.5 ясно видно, что функция А(В + С) эквивалентна функции АВ + АС. Несмотря на эту эквивалентность, схема на рис. 3.5, б проще, чем схема на рис. 3.5, я, поскольку содержит меньше вентилей.

Обычно разработчик исходит из определенной булевой функции, а затем применяет к ней законы булевой алгебры, чтобы найти более простую функцию, эквивалентную исходной. На основе полученной функции можно конструировать схему.

Чтобы использовать данный подход, нужно знать некоторые соотношения (законы) булевой алгебры, которые показаны в табл. 3.1. Интересно отметить, что каждое соотношение имеет две формы. Одну форму можно получить из другой, меняя И на ИЛИ и 0 на 1. Все соотношения можно легко доказать, составив для них таблицы истинности. Почти во всех случаях результаты очевидны, за исключением соотношения Де Моргана, соотношения поглощения и дистрибутивного соотношения. Соотношение Де Моргана может быть расширено на выражения с более чем двумя переменными, например, АВС = А + В + С.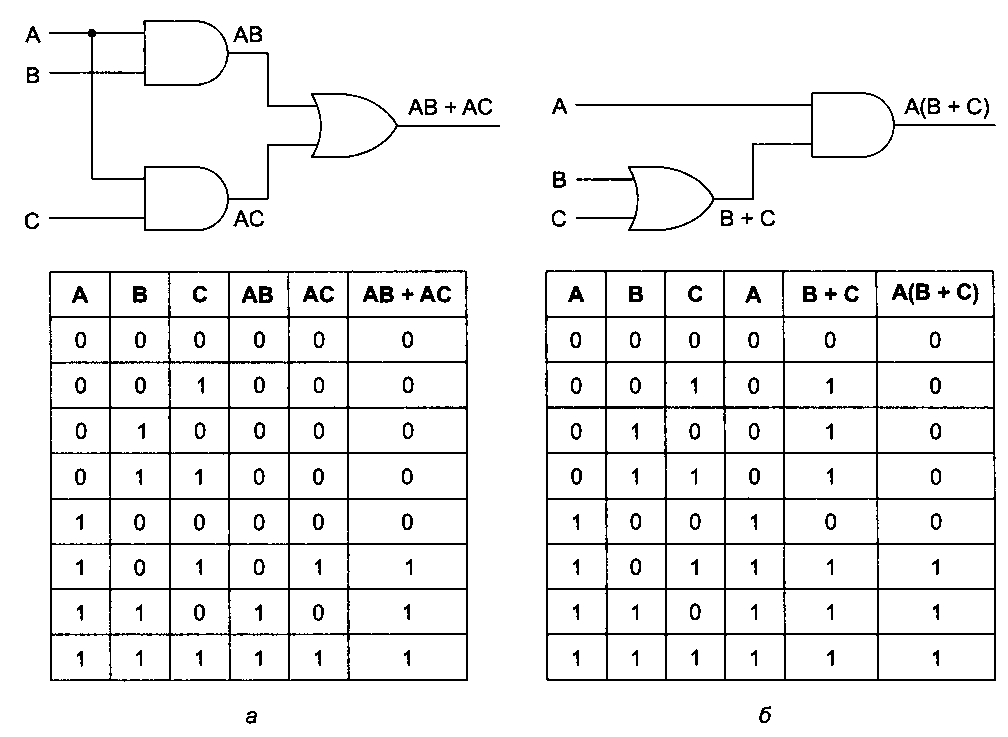

Рис. 3.5. Две эквивалентные функции: АВ + АС (а); А(В + С) (б) Таблица 3.1. Некоторые соотношения булевой алгебры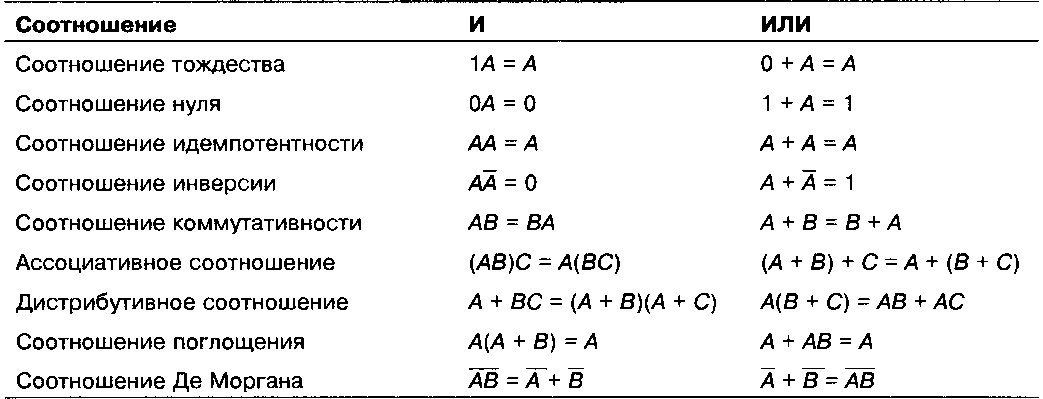

Соотношение Де Моргана предполагает альтернативную запись. На рис. 3.6, а форма И дается с отрицанием, которое показывается с помощью инвертирующих входов и выходов. Таким образом, вентиль ИЛИ с инвертированными входными сигналами эквивалентен вентилю НЕ-И. Из рис. 3.6, б, который иллюстрирует вторую форму соотношения Де Моргана, ясно, что вместо вентиля НЕ-ИЛИ можно нарисовать вентиль И с инвертированными входами. Путем отрицания обеих форм соотношения Де Моргана мы приходим к эквивалентным представлениям вентилей И и ИЛИ (рис. 3.6, в и г). Аналогичные символиче ские изображения существуют для разных форм соотношения Де Моргана (например, я-входовый вентиль НЕ-И становится вентилем ИЛИ с инвертированными входами).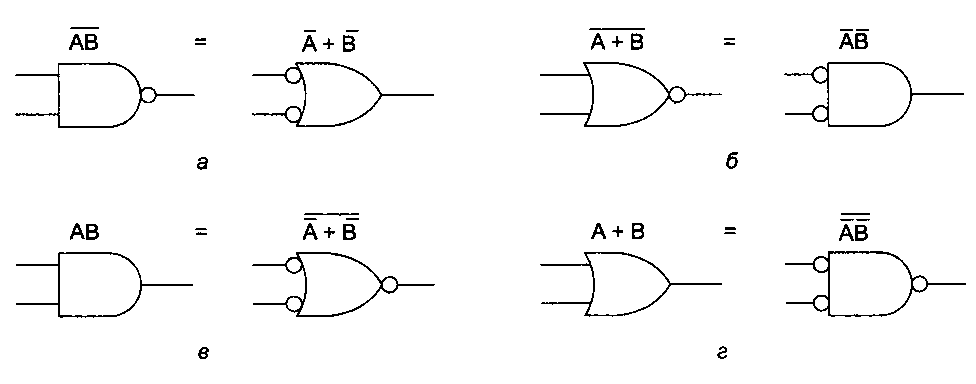

Рис. 3.6. Альтернативные представления некоторых вентилей: НЕ-И (а); НЕ-ИЛИ (б);

И (б); ИЛИ (г)

Использовав уравнения, указанные на рис. 3.6, и аналогичные уравнения для многовходовых вентилей, можно легко преобразовать сумму произведений в форму только из вентилей НЕ-И или только из вентилей НЕ-ИЛИ. В качестве примера рассмотрим функцию ИСКЛЮЧАЮЩЕЕ ИЛИ (рис. 3.7, а). Стандартная схема, выражающая сумму произведений, показана на рис. 3.7, б. Чтобы перейти к форме НЕ-И, нужно линии, соединяющие выходы вентилей И с входом вентиля ИЛИ, нарисовать с инвертирующими входами и выходами, как показано на рис. 3.7, е.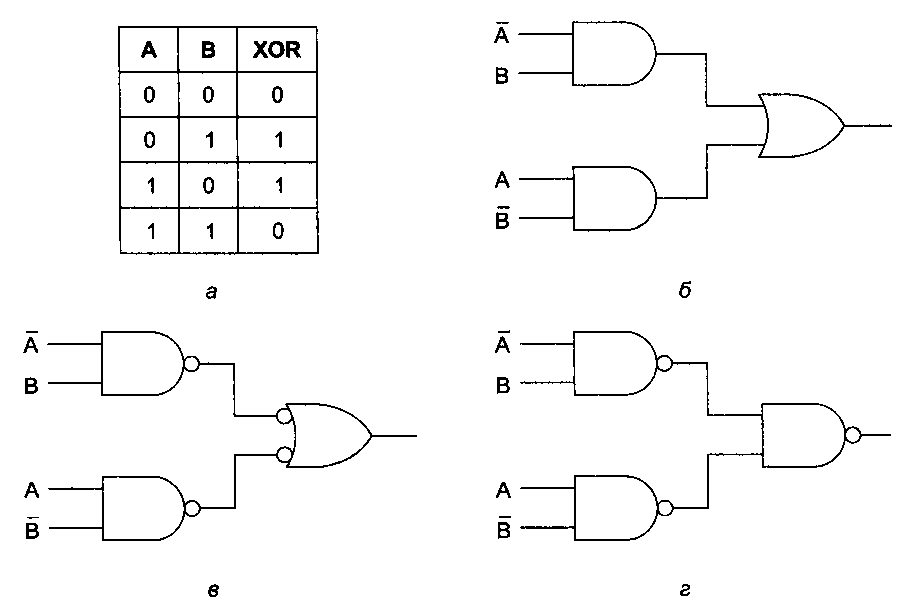

Рис. 3.7. Таблица истинности для функции ИСКЛЮЧАЮЩЕЕ ИЛИ (а). Три схемы для вычисления этой функции (б), (в), (г)