Реклама

Наш канал:

Таненбаум Э.- Архитектура компьютера. стр.123

Схема содержит четыре вентиля И, по одному для каждого члена в уравнении для М (то есть по одному для каждой строки в таблице истинности с результатом 1). Каждый вентиль И вычисляет одну из указанных строк таблицы истинности. В конце концов, все данные произведения суммируются (имеется в виду операция ИЛИ) для получения конечного результата.

Посмотрите на рис. 3.3, б. В этой книге мы будем использовать следующее соглашение: если две линии на рисунке пересекаются, связь подразуме вается только в том случае, если на пересечении расположена жирная точка. Например, выход вентиля 3 пересекает все 6 вертикальных линий, но связан он только с линией С. Отметим, что другие авторы могут использовать другие соглашения.

Из рис. 3.3 должно быть ясно, как получить схему для любой булевой функции:

1. Составить таблицу истинности для данной функции.

2. Включить в схему инверторы, чтобы иметь возможность инверсии каждого входного сигнала.

3. Нарисовать вентиль И для каждой строки таблицы истинности с результатом 1.

4. Соединить вентили И с соответствующими входными сигналами.

5. Вывести выходы всех вентилей И и направить их на вход вентиля ИЛИ.

Мы показали, как реализовать любую булеву функцию с помощью вентилей НЕ, И и ИЛИ. Однако гораздо удобнее строить схемы с использованием одного типа вентилей. К счастью, можно легко преобразовать схемы, построенные по предыдущему алгоритму, в форму НЕ-И или НЕ-ИЛИ. Чтобы осуществить такое преобразование, все, что нам нужно, — это реализовать вентили НЕ, И и ИЛИ с помощью какого-нибудь одного типа вентилей. На рисунке 3.4 показано, как это сделать на базе вентиля НЕ-И или НЕ-ИЛИ. Отметим, что существуют и другие варианты подобного преобразования.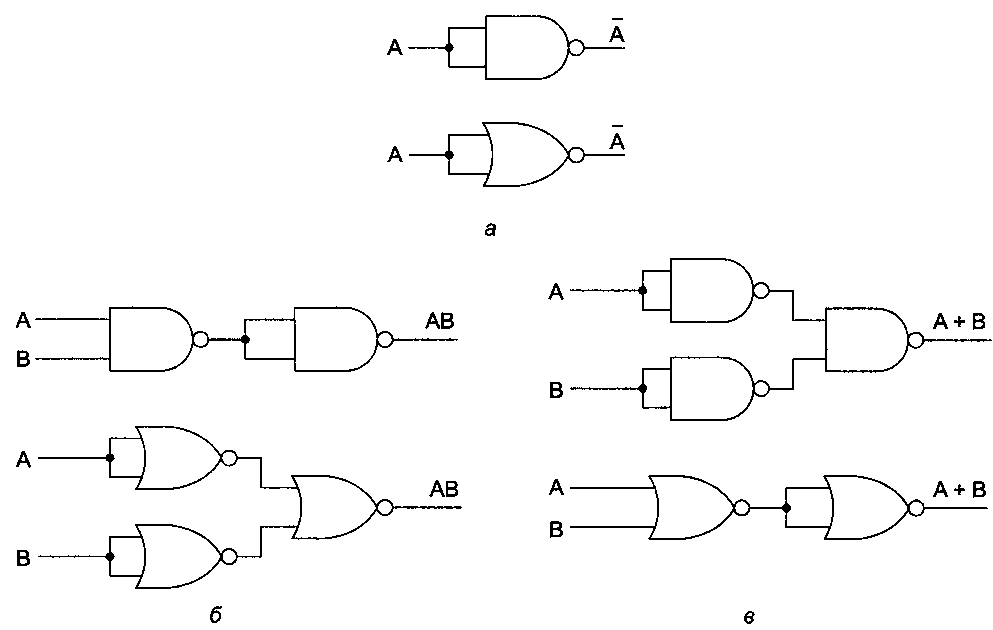

Рис. 3.4. Конструирование вентилей НЕ (а), И (б) и ИЛИ (в) только на базе вентиля НЕ-И или НЕ-ИЛИ

Для того чтобы реализовать булеву функцию только на базе вентиля НЕ-И или НЕ-ИЛИ, можно сначала следовать описанному алгоритму, сконструировав схему с вентилями НЕ, И и ИЛИ. Затем нужно заменить многовходо-вые вентили эквивалентными схемами на двухвходовых вентилях. Например, А + В + С + В можно поменять на (А + В) + (С + И), использовав три двухвходовых вентиля. Затем вентили НЕ, И и ИЛИ заменяются схемами, изображенными на рис. 3.4.

Хотя такая процедура и не приводит к оптимальным схемам с точки зрения минимального числа вентилей, она демонстрирует, что подобное преобразование осуществимо. Вентили НЕ-И и НЕ-ИЛИ считаются полными, потому что каждый из них позволяет вычислить любую булеву функцию. Ни один другой вентиль не обладает таким свойством, вот почему именно эти два типа вентилей предпочтительнее при построении схем.

Эквивалентность схем

Разработчики схем часто стараются сократить число вентилей, чтобы снизить цену, уменьшить занимаемое схемой место, сократить потребление энергии и т. д. Чтобы упростить схему, разработчик должен найти другую схему, которая может вычислять ту же функцию, но при этом требует меньшего количества вентилей (или может работать с более простыми вентилями, например, двухвходовыми вместо четырехвходовых). Булева алгебра является ценным инструментом в поиске эквивалентных схем.