Реклама

Наш канал:

Таненбаум Э.- Архитектура компьютера. стр.122

нельзя описать, дав таблицу значений этой функции для всех возможных значений входных переменных, поскольку каждая переменная может принимать бесконечное число значений.

На рис. 3.3, а показана таблица истинности для булевой функции от трех переменных: М = /(А, В, С). Это функция большинства, которая принимает значение 0, если большинство переменных равны 0, или 1, если большинство переменных равны 1. Хотя любая булева функция может быть определена с помощью таблицы истинности, с возрастанием количества переменных такой тип записи становится громоздким. Поэтому вместо таблиц истинности часто используется другой вариант записи.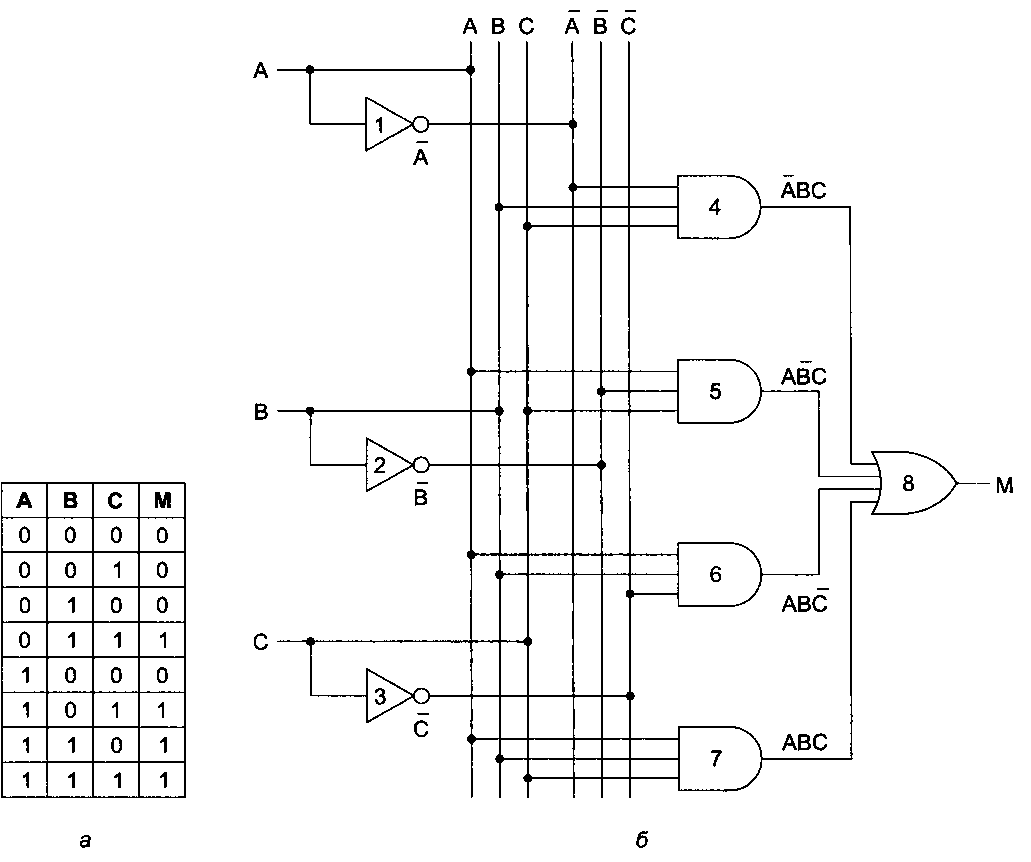

Рис. 3.3. Таблица истинности для функции большинства от трех переменных (а); схема реализации этой функции (б)

Чтобы увидеть этот другой тип записи, отметим, что любую булеву функцию можно определить, указав, какие комбинации значений входных переменных приводят к единичному значению функции. Для функции, приведенной на рис. 3.3, а, существует 4 комбинации переменных, которые дают единичное значение функции. Мы будем рисовать черту над переменной, показывая, что ее значение инвертируется. Отсутствие черты означает, что значение переменной

не инвертируется. Кроме того, мы будем использовать знак умножения (точку) для обозначения булевой функции И (этот знак может опускаться) и знак сложения (+) для обозначения булевой функции ИЛИ. Например, ABC принимает значение 1, только если Л = 1,£ = 0иС=1. Кроме того, AB + ВС принимает значение 1, только если (А = 1 и В = 0) или (В = 1 и С== 0). ^таблице на рис. 3.3, а функция принимает значение 1 в четырех строках: А В С, А В С, ABC и ABC. Функция М принимает значение истины (то есть 1), если одно из этих четырех условий истинно. Следовательно, мы можем написать

М - ABC + ABC + ABC + ABC.

Это компактная запись таблицы истинности. Таким образом, функцию от п переменных можно описать суммой максимум 2п произведений, при этом в каждом произведении будет по п множителей. Как мы скоро увидим, такая формулировка особенно важна, поскольку она позволяет реализовать данную функцию с использованием стандартных вентилей.

Важно понимать различие между абстрактной булевой функцией и ее реализацией с помощью электронной схемы. Булева функция состоит из переменных, например, А, В и С, г, также из операторов И, ИЛИ и НЕ. Булева функция описывается с помощью таблицы истинности или специальной записи, например:

F = АВС + ABC.

Булева функция может быть реализована электронной схемой (часто различными способами) с использованием сигналов, которые представляют входные и выходные переменные, и вентилей, например, И, ИЛИ и НЕ.

Реализация булевых функций

Как было отмечено ранее, представление булевой функции в виде суммы максимум 2п произведений делает возможной реализацию этой функции. На рис. 3.3, б входные сигналы А, В и С показаны с левой стороны, а функция М, полученная на выходе, — с правой. Поскольку необходимы дополнительные величины (инверсии) входных переменных, для их получения сигнал проходит через инверторы 1, 2 и 3. Чтобы сделать рисунок понятней, мы нарисовали 6 вертикальных линий, 3 из которых связаны с входными переменными, 3 другие — с их инверсиями. Эти линии обеспечивают передачу входного сигнала к вентилям. Например, вентили 5, 6 и 7 на входе получают сигнал А. В реальной схеме эти вентили, вероятно, будут непосредственно соединены проводом с А без каких-либо промежуточных вертикальных проводов.