Проблема возникает в том случае, если абсолютное значение (модуль) результата меньше самого маленького нормализованного числа с плавающей точкой, которое можно представить в этой системе. Раньше аппаратное обеспечение действовало одним из двух способов: либо устанавливало результат на 0, либо вызывало ошибку потери значимости. Ни один из этих двух способов не является удовлетворительным, поэтому в стандарт IEEE введены ненормализованные
числа. Эти числа имеют экспоненту 0 и мантиссу, представленную следующими 23 или 52 битами. Неявный бит 1 слева от двоичной точки превращается в 0. Ненормализованные числа можно легко отличить от нормализованных, поскольку у последних не может быть нулевой экспоненты.
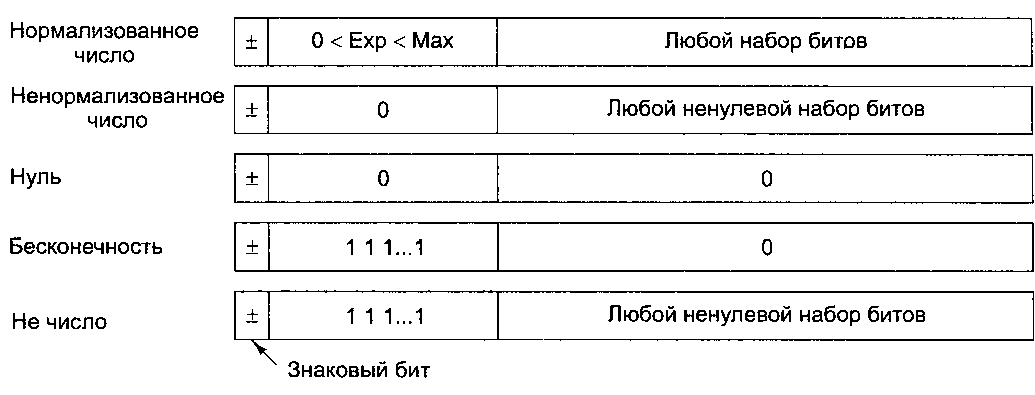
Рис. Б.4. Числовые типы стандарта IEEE
Самое маленькое нормализованное число с одинарной точностью содержит 1 в экспоненте и 0 в мантиссе и представляет 1,0 х 2~126. Самое большое ненормализованное число содержит 0 в экспоненте и все единицы в мантиссе и представляет примерно 0,9999999 х 2~127, то есть почти то же самое число. Следует отметить, что это число содержит только 23 бита значимости, а все нормализованные числа — 24 бита.
По мере уменьшения результата при дальнейших вычислениях экспонента по-прежнему остается равной 0, а первые несколько битов мантиссы превращаются в нули, что уменьшает и значение, и число значимых битов мантиссы. Самое маленькое ненулевое ненормализованное число содержит 1 в крайнем правом бите, а все остальные биты равны 0. Экспонента представляет 2~127, а мантисса — 2~23, поэтому значение равно 2~150. Такая схема предусматривает постепенное исчезновение значимых разрядов, а не перескакивает на 0, когда результат не удается выразить в виде нормализованного числа.
В этой схеме присутствует два нуля, положительный и отрицательный, определяемые по знаковому биту. Оба имеют экспоненту 0 и мантиссу 0. Здесь тоже бит слева от двоичной точки по умолчанию равен 0, а не 1.
Простого решения проблемы переполнения нет. Для этого существует специальное представление бесконечности: с экспонентой, содержащей все единицы, и мантиссой, равной 0. Это число можно использовать в качестве операнда. Оно подчиняется обычным математическим правилам для бесконечности. Например, бесконечность и любое число в сумме дают бесконечность. Конечное число, деленное на бесконечность, равно 0. Любое конечное число, разделенное на 0, стремится к бесконечности.
А что получится, если бесконечность разделить на бесконечность? Результат не определен. Для такого случая существует другой специальный формат — не число (Not a Number, NaN). Его тоже можно использовать в качестве операнда.
Вопросы и задания
1. Преобразуйте следующие числа в формат стандарта IEEE с одинарной точностью. Результаты представьте в восьми шестнадцатеричных разрядах.
1) 9;
2) 5/32;
3) -5/32;
4) 6,125.
2. Преобразуйте следующие числа с плавающей точкой одинарной точности из шестнадцатеричной в десятичную систему счисления:
1) 42Е28000Н;
2) 3F880000H;
3) 00800000Н;
4) C7F00000H.