Реклама

Наш канал:

Таненбаум Э.- Архитектура компьютера. стр.532

Преобразование десятичных чисел в двоичные можно совершать двумя разными способами. Первый способ непосредственно вытекает из определения двоичных чисел. Самая большая степень двойки, меньшая, чем число, вычитается из этого числа. Та же операция проделывается с полученной разностью. Когда число разложено по степеням двойки, двоичное число может быть получено следующим образом. Единички ставятся в тех позициях, которые соответствуют полученным степеням двойки, а нули — во всех остальных позициях.

Второй способ — деление числа на 2. Частное записывается непосредственно под исходным числом, а остаток (0 или 1) записывается рядом с частным. То же проделывается с полученным частным. Процесс повторяется до тех пор, пока не останется 0. В результате должно получиться две колонки чисел — частных и ос татков. Двоичное число можно считать из колонки остатков снизу вверх. На рис. А.4 показано, как происходит преобразование из десятичной в двоичную систему.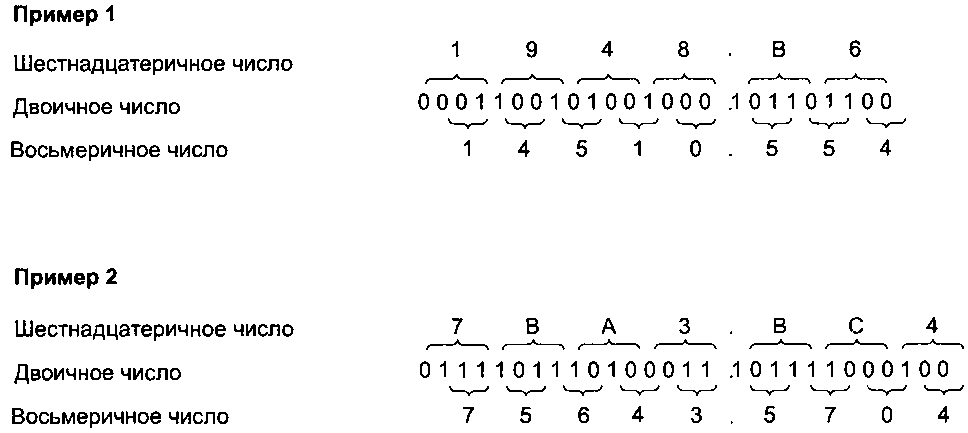

Рис. А.З. Примеры преобразования из восьмеричной системы счисления в двоичную и из

шестнадцатеричной в двоичную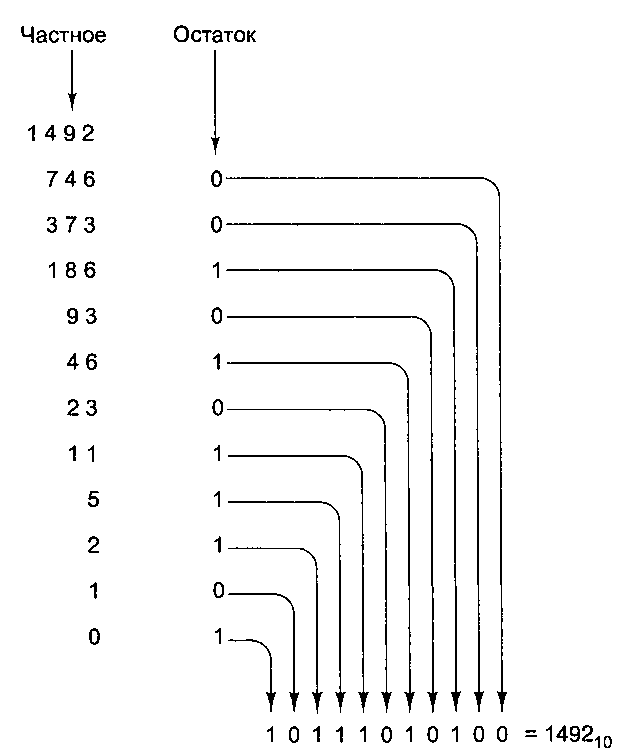

Рис. А.4. Преобразование десятичного числа 1492 в двоичное путем последовательного деления (сверху вниз). Например, 93 делится на 2, получается 46 и остаток 1. Остаток записывается в строку снизу

Двоичные числа можно преобразовывать в десятичные двумя способами. Первый способ — суммирование степеней двойки, которые соответствуют битам 1 в двоичном числе. Например:

10110 = 24 + 22 + 21 = 16 + 4 + 2 = 22.

Во втором способе двоичное число записывается вертикально по одному биту в строке, крайний левый бит находится внизу. Самая нижняя строка — это строка 1, затем идет строка 2 и т. д. Десятичное число строится напротив этой колонки. Сначала обозначим строку 1. Элемент строки п состоит из удвоенного элемента строки п - 1 плюс бит строки п (0 или 1). Элемент, полученный в самой верхней строке, и будет ответом. Метод иллюстрирует рис. А.5.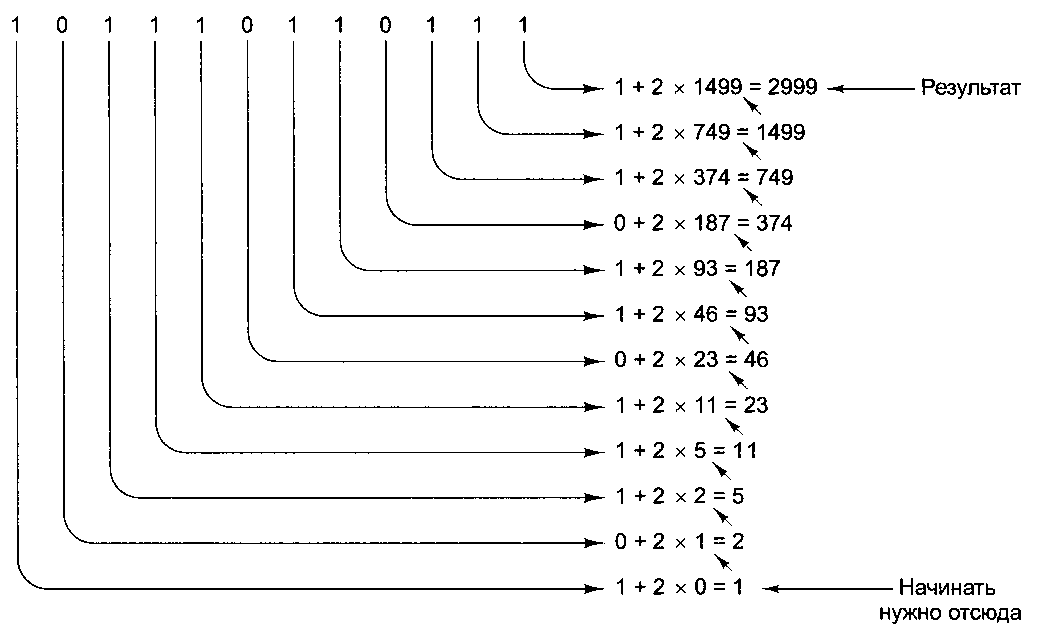

Рис. А.5. Преобразование двоичного числа 101110110111 в десятичное путем последовательного удваивания снизу вверх. В каждой следующей строке удваивается

значение предыдущей строки и прибавляется соответствующий бит. Например, 374 умножается на 2 и прибавляется бит соответствующей строки (в данном случае 1).

В результате получается 749

Преобразование из десятичной в восьмеричную или шестнадцатеричную систему можно выполнить либо путем преобразования сначала в двоичную, а затем в нужную нам систему, либо путем вычитания степеней 8 или 16.

Отрицательные двоичные числа

На протяжении всей истории цифровых компьютеров для представления отрицательных чисел использовались 4 различные системы. Первая из них называется системой со знаком. В такой системе крайний левый бит — это знаковый бит

(О — плюс, 1 — минус), а оставшиеся биты показывают абсолютное значение числа.

Во второй системе, которая называется дополнением до единицы, тоже присутствует знаковый бит (0 — плюс, 1 — минус). Чтобы сделать число отрицательным, нужно заменить каждую единицу нулем и каждый ноль единицей. Это относится и к знаковому биту. Система дополнения до единицы уже устарела.